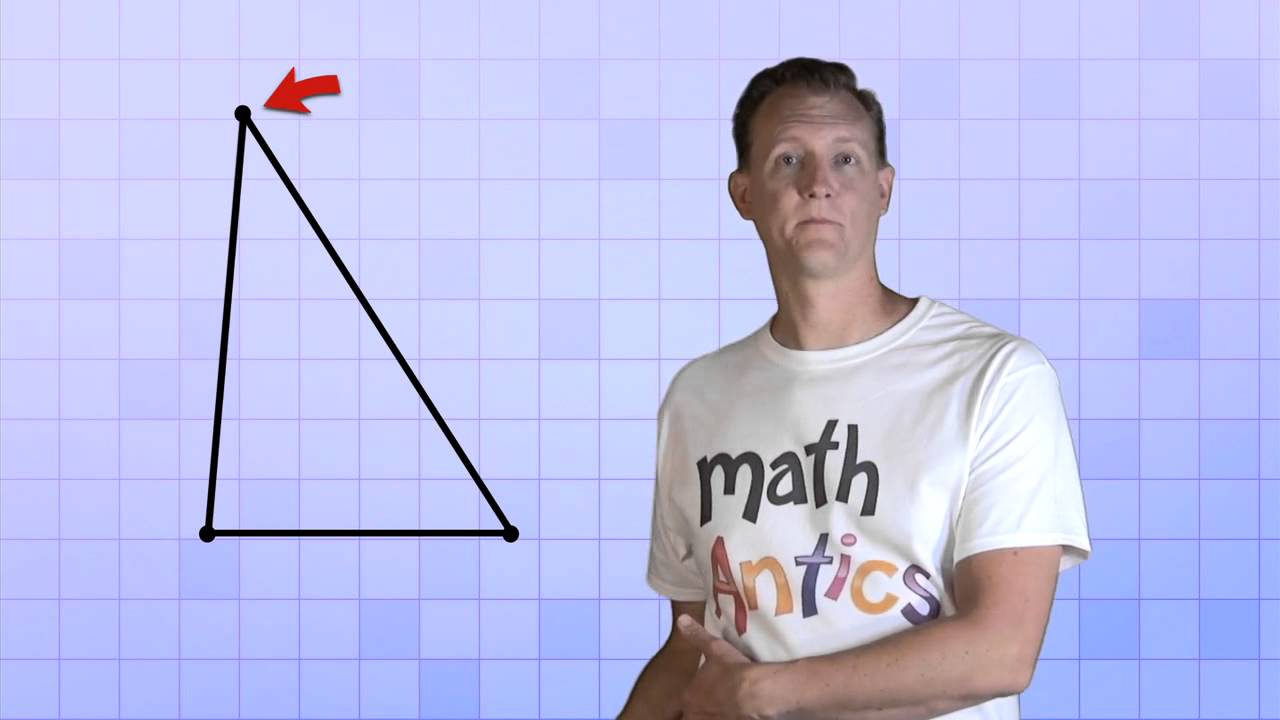
A triangle is a three-sided polygon that is at times (however not generally) called a triangle. Each triangle has three sides and three points, some of which might be equivalent. On account of a right calculated triangle, extraordinary names are given to the sides of a triangle, with the side inverse to the right point called the hypotenuse and the other different sides called the legs. All triangles are curved and bicentered. That piece of the plane that encompasses the triangle is known as the inside of the triangle, while the rest is the outside.
Click here https://petsbee.com/
The investigation of triangles is some of the time alluded to as triangle math, and a rich field of calculation is loaded with delightful outcomes and surprising associations. In 1816, while concentrating on the Brocard points of a triangle, Creeley said, “It is without a doubt shocking that a basic figure, for example, a triangle is so unlimited in properties. The number of not yet obscure properties that might different figures at any point have?”
Here you can find similar topics like these 36 inches in feet
Triangle
It is normal to name the vertices of a triangle as A, B, C (or A_1, A_2, A_3) in counterclockwise request. Then the vertex points are given similar images as the actual vertices. The images alpha, beta, gamma (or alpha_1, alpha_2, alpha_3) are additionally some of the time utilized (for instance, Johnson 1929), however this show came about in the trilinear arranges alpha:beta:gamma, etc. Not there. suggested. Inverse sides of A, B, and C (or A_1, A_2, A_3) are then named A, B, C (or A_1, A_2, A_3), with these images likewise demonstrating the lengths of the sides (for example that the images on the vertices demonstrate themselves as well as the vertex points relying upon the unique situation).
Triangle
A triangle is supposed to be intense calculated in the event that each of the three of its points are intense, an uncaring triangle is called an unfeeling triangle and a right calculated triangle is known as a right calculated triangle. A triangle whose everything sides are equivalent is called symmetrical, a triangle whose different sides are equivalent is called isosceles, and a triangle whose all sides are not the same as one another is called scalene. A triangle can be at the same time right calculated and isosceles, in which case it is known as an isosceles right calculated triangle.
The semi-border of a triangle is characterized as a portion of its edge,
s = 1/2p
(1)
= 1/2(a+b+c).
(2)
The region of a triangle can be given by Heron’s recipe
delta = sqrt(s (s-a) (s-b) (s-c)).
(3)
There are numerous different recipes for the triangle region also.
Meanings of semiparameters lead to definitions
s_a = 1/2(b+c-a)
(4)
= s-a
(5)
= arcot(1/2a)
(6)
s_b = 1/2(c+a-b)
(7)
= s-b
(8)
= arcot(1/2b)
(9)
s_c = 1/2(a+b-c)
(10)
= s-c
(1 1)
= arcot(1/2 c),
(12)
where r is the span. There is a comparable arrangement of relations for the Conway triangle documentation S, S_A, S_B and S_C.
Triangle Point
The amount of the points in a triangle is 180° = pi radians (to some degree in Euclidean math; this assertion doesn’t hold in non-Euclidean calculation). It tends to be introduced as follows. In the above chart DAE∥BC (DAE be lined up with BC), then, at that point, points alpha and beta fulfill alpha=∠DAB=∠ABC and beta=∠EAC=∠ACB, as demonstrated. On adding gamma, it follows
alpha+beta+gamma=180 degrees,
(13)
Since the amount of the points of a line fragment should be equivalent to two right points. In this way, the amount of the points in a triangle is likewise 180 degrees.
Triangle Equal Line
Assuming a line lined up with one side of a triangle is drawn so it converges the other different sides, it separates them relatively, i.e.,
(Hatchet)/(XC)=(BY)/(YC)
(14)
(Jurgensen 1963, p. 251). As such, the line lined up with one side of the triangle meeting the other different sides shapes a similar triangle as in the past.
The reasonable side lengths for a triangle a, b, and c are given by the arrangement of disparities a>0, b>0, c>0, and a+b>c, b+c>a, a+c>b , an assertion contained in the purported triangle imbalance. The points and sides of a triangle likewise fulfill a variety of other wonderful triangle imbalances.
Indicating two points An and B and a side exceptionally decides a triangle with region
Delta = (a^2sinBsinC)/(2sinA)
(15)
= (a^2sinBsin(pi-A-B))/(2sinA)
(16)
(AAS Hypothesis). Determining a point A, a side c, and a point B explicitly assigns a triangle with region
delta=(c^2)/(2(cotA+cotB))
(17)
(ASA hypothesis). Given a triangle with different sides, a more modest and c more prominent, and a known point A, intense and inverse a, in the event that sinA<a/c, there are two potential triangles. If sinA=a/c, is a potential triangle. If sinA>a/c, there are no potential triangles. This is the ASS hypothesis. Let a be the length of the base and h be the level. Then
delta = 1/2ah
(18)
= 1/2acsinB
(19)
(SAS Hypothesis). At last, in the event that each of the three sides are indicated, a remarkable not entirely set in stone by the area given by Heron’s recipe or by
delta=(abc)/(4r),
(20)
where R is the sweep. This is the SSS hypothesis.
trilinear arranges
In triangle math, it is frequently extremely advantageous to utilize trios of directions characterized comparative with distance.
Guaranteed supposed reference is acquired from each side of the triangle. One type of such organizes is known as trilinear facilitates alpha:beta:gamma, in which all directions have equivalent signs comparing to the inside of the triangle, a zero relating to a point on one side, two directions relating to a vertex, zero. , and the directions are various signs comparing to the outside of the triangle.
Triangle Development
The erect and compass development of the triangle can be achieved as follows. In the above figure, accept OP_0 as a sweep and draw OB_|_OP_0. Then, at that point, separate OB and develop P_2P_1∥OP_0. The symmetrical triangle DeltaP_1P_2P_3 when BO is extended to find P_3 gives. Another development continues by drawing a circle of wanted sweep r focused at a point O. Pick a point B on the outline of the circle and draw one more circle of span r focused at B. Two circles meet at two focuses P_1 and P_2, and P_3 is the second place where the line B_O crosses the principal circle.
Intercircular Circle
In Recommendation IV.4 of Components, Euclid told the best way to engrave a circle (incircle) in a given triangle by finding the middle I as the place of crossing point of the point bisectors. In Recommendation IV.5, he told the best way to surround a circle (roundabout) around a given triangle, setting the circumcentre O as the place of crossing point of the opposite bisectors. Dissimilar to an ordinary polygon with n>=4 sides, a triangle generally has one circumcircle and one incircle. Such polygons are called bicentral polygons.
A triangle with sides a, b, and c can be developed by choosing the vertices (0, 0), (c,0), and (x,y), then tackling
x^2+y^2 = b^2
(21)
(x-c)^2+y^2 = a^2
(22)
to get together
x = (- a^2+b^2+c^2)/(2c)
(23)
= BCOSA
(24)
y = +/ – (square ((- a+b+c)(a-b+c)(a+b-c)(a+b+c))/(2c)
(25)
= +/- (2 delta)/c.
(26)
The points of the triangle fulfill the law of cosines
cosA=(b^2+c^2-a^2)/(2bc),
(27)
With all
cotA=(b^2+c^2-a^2)/(4Delta)
(28)
where delta is the region (Johnson 1929, p. 11, with the missing square sign added). The last option gives delightful personality
cotA+cotB+cotC=(a^2+b^2+c^2)/(4Delta).
(29)
at the same time,
tanA+tanB+tanC=tanAtanBtanC
(30)
(F.J. ND, p. 206; Borchard and Perot 1930) and
cotBcotC+cotCcotA+cotAcotB=1
(31)
tanAcotBcotC+tanBcotCcotA+tanCcotAcotB
=tanA+tanB+tanC+2(cotA+cotB+cotC)
(32)
(Siddons and Hughes 1929), and
cot(1/2a)+cot(1/2b)+cot(1/2c)
= cot(1/2a)cot(1/2b)cot(1/2c).
(33)
Extra sources incorporate
cos^2A+cos^2B+cos^2C+2cosAcosBcosC=1,
(34)
What’s more,
cos(nA) = cos[n(B+C)]
(35)
cos(nB) = cos[n(A+C)]
(36)
cos(nc) = cos[n(a+b)]
(37)
for even n (Weisstein, January 31, 2003 and Walk 3, 2004).
The geometrical elements of half points in a triangle can be communicated as the sides of the triangle:
cos(1/2A) = sqrt((s(s-a))/(bc))
(38)
sin(1/2A) = sqrt(((s-b)(s-c))/(bc))
(39)
tan(1/2A) = sqrt(((s-b)(s-c))/(s(s-a))),
(40)